Prashant Gupta

Prashant Gupta

Research Scientist, Ph.D. in Mathematics

Space Filling Curve Based Graph Partitioning Approach for Non-Metric Lawn Mowing And 3D Printing Problems

1 minute read

Published:

Overview

We formulated the 3d printing problem. The 3D printing problem is the same as the lawn mowing problem. We showed minimum turn lawn mowing / 3D printing problem is NP-hard. It is known minimum length lawn mowing / 3D printing problem is NP-hard 1. Suppose we are solving the lawn mowing problem on space $X$. It is difficult to design an approximation algorithm, if

  1. Turn cost is involved. Since the turn cost problem does not form a metric.
  2. Edge weight in the dual graph of $X$ is not a metric.

Our Work

We may want to solve the exact problem using MIP. But MIPs are hard to solve for large instances of the problem. This motivated the development of our work.

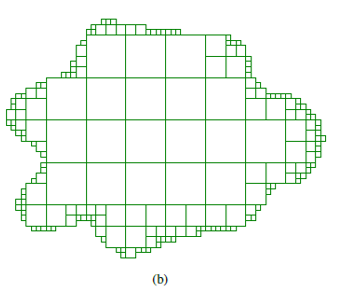
  1. Find integral orthogonal polygon (IOP) for a given polygon.
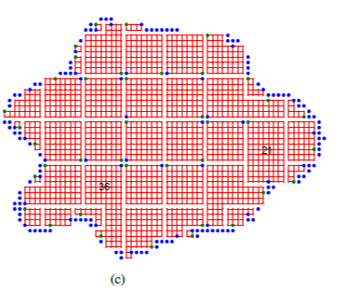
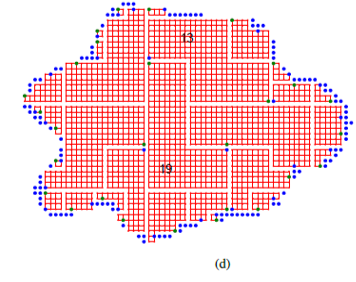
  2. Partition the dual graph of the IOP into multiple dual graphs using a space-filling curve. Each dual graph has its enter and exit vertices. Further, we guarantee there exists a Hamiltonian path for each dual graph between entry and exit vertices.
  3. We used MTZ formulation with turn cost to solve the Hamiltonian path problem for each dual graph.
  4. Connect these Hamiltonian paths between dual graphs based on the space-filling curve sequence. We were able to solve problems with total $812,733$ nodes of a bunny over $360$ layers and $799,716$ nodes of buddha over $169$ layers.

For more details check out our work SFCDecomp: Multicriteria Optimized Tool Path Planning in 3D Printing using Space-Filling Curve Based Domain Decomposition

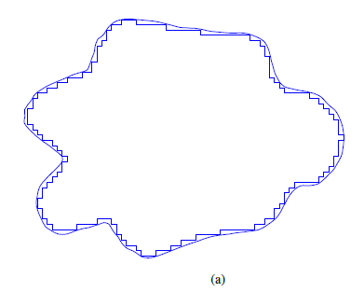
An illustration for a general polygon is shown below.

Figure 1
Figure 2
Figure 3
Figure 4
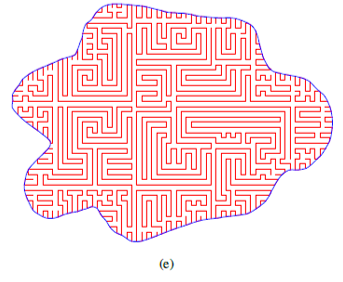Figure 5
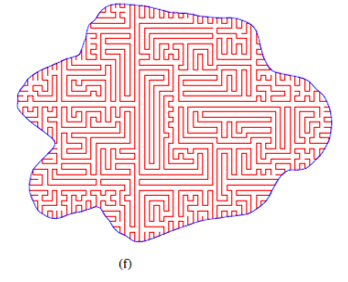Figure 6

Images of some 3d printed layers of the bunny.

Figure 7
Figure 8
Figure 9

Images of tool path of some layers of the bunny.

Figure 10
Figure 11

References

  1. E. M. Arkin, S. P. Fekete, J. S. B. Mitchell, Approximation algorithms for lawn mowing and milling, Computational Geometry 17 (1-2) (2000) 25–50. ↩

You May Also Enjoy

Data exploration using Mapper

1 minute read

Published:

I am currently working on a paper to build a new mathematical technique for Topological Data Analysis. I used this technique to build a TDA mapper tool. This post is to give basic intuition about the mapper. Mapper is used to get a higher-level understanding of the structure of the data. It is used to visualize the shape of the data in higher dimensions. Given a mapper representation of $3$D point cloud (Points are uniformly distributed) belongs to a set of animals (horse, lion, cat, camel, elephant, flamingo). Each ball in the mapper represents a cluster and the edge between balls implies common points between corresponding clusters (intuition not definition of the mapper).

Sentence Classification using CNN

5 minute read

Published:

ABSTRACT

Convolution Neural Networks are typically used in computer vision problems like image classification. Most of the computer vision systems todays at its core are based on CNNs from photo tagging to self driving cars. However we are going to look at the application of CNNs in NLP(Natural Language Processing).