Euler Transformation of Polyhedral Complexes

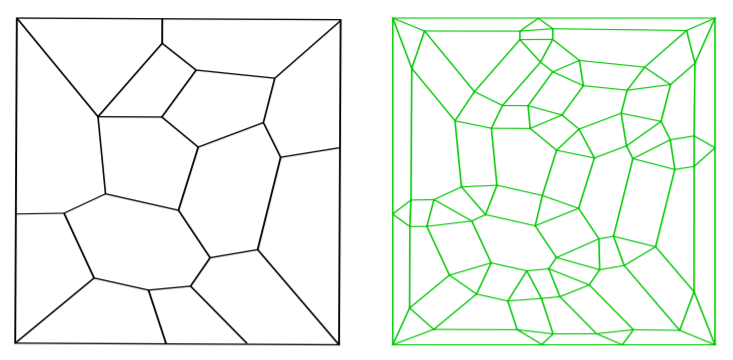
We propose an Euler transformation that transforms a given $d$-dimensional cell complex $K$ for $d=2,3$ into a new $d$-complex $\hat{K}$ in which every vertex is part of a uniform even number of edges. Hence every vertex in the graph $\hat{G}$ that is the $1$-skeleton of $\hat{K}$ has an even degree, which makes $\hat{G}$ Eulerian, i.e., it is guaranteed to contain an Eulerian tour. Meshes whose edges admit Eulerian tours are crucial in coverage problems arising in several applications including 3D printing and robotics. For $2$-complexes in $R^2$ ($d=2$) under mild assumptions (that no two adjacent edges of a $2$-cell in $K$ are boundary edges), we show that the Euler transformed $2$-complex $\hat{K}$ has a geometric realization in $R^2$, and that each vertex in its $1$-skeleton has degree $4$. We bound the numbers of vertices, edges, and $2$-cells in $\hat{K}$ as small scalar multiples of the corresponding numbers in $K$. We prove corresponding results for $3$-complexes in $R^3$ under an additional assumption that the degree of a vertex in each $3$-cell containing it is $3$. In this setting, every vertex in $\hat{G}$ is shown to have a degree of $6$. We also presents bounds on parameters measuring geometric quality (aspect ratios, minimum edge length, and maximum angle) of $\hat{K}$ in terms of the corresponding parameters of $K$ (for $d=2,3$). Finally, we illustrate a direct application of the proposed Euler transformation in additive manufacturing.

Download paper here